You are here: GSI Wiki>TOS/BunchBucket Web>BunchBucketDocumentation>BunchBucketDocuments>BunchBucketTestsMeasurements>BunchBucketTestMeasurement12 (2023-06-20, dbeck)Edit Attach
June 2023: Testing Precision in the Production System
Table of ContentsTL;DR
If you are not interested in details: The precision 'as-is' seems to exceeds specifications and the overall system is very stable.Introduction
So far, the productive bunch-2-bucket system only provided timestamps with a 1ns granularity. As the granularity can not be changed easily, the idea is to enhance the precision by using not only a single timestamp of the positive zero-crossing of the h=1 signal. Instead, multiple samples of consecutive zero-crossing are timestamped. Then, sub-ns precision is obtained by 'fitting' the theoretical h=1 signal - that has a known, fixed frequency - to the measured samples (details can be found here). A proof-of-principle of this method has been demonstrated in this measurement. During the winter 2022/2023, the relevant changes have been implement through the control system stack from ParamModi -> Settings Management -> FESA -> b2b system. After a test in the integration system, the changes have been deployed to the production system an tested during the equipment test and dry-run in May and June 2023. The results are reported here.Setup
Procedure
The procedure is similar to the one described here. As a true bunch-2-bucket transfer shall be performed, an additional phase measurement is done at the injection ring. From the known frequencies of the h=1 DDS signals, the b2b system derives the frequency beating patterns and predicts phase matching of the two DDS signals. For each transfer, three phase measurements are done in each ring:- beginning of flat-top
- at transfer (extraction or injection)
- end of flat-top
- extraction ring: phase difference; measurements at start and end of flat top
- injection ring: phase difference; measurements at start and end of flat top
- at transfer: phase difference; two measurements done at transfer; one in the injection and another one in the extraction ring
SIS18 -> ESR
The measurement was done from 2-5 June 2023. The following parameters were used- SIS18
- Pattern SIS18_FAST_20220601_181223
- Trev = 1433.563551707 ns (true DDS value)
- ESR
- Pattern ESR_EXP22_05_Au78_150-30-10_CRYRING_BB_MIT_Line
- Trev = 716.930952630 ns (true DDS value)
- frequency beating
- h=2 (SIS18) -> h=1 (ESR)
- period 3.444 ms
- phase difference per rf-period: 149 ps (0.075° @ h=2, SIS18)
- multi-beat-tune = yes
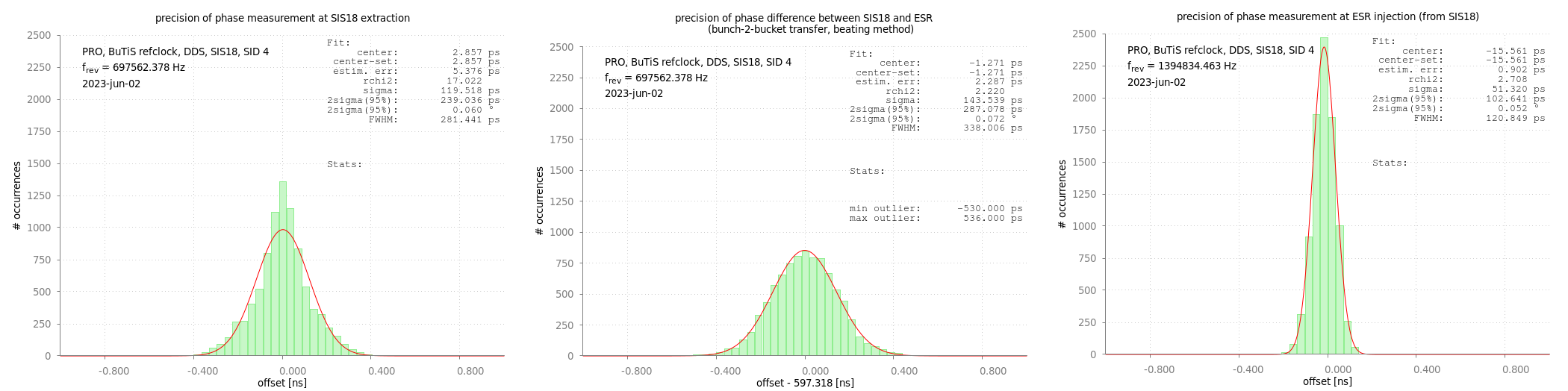 Figure: Measured phase differences. The differences are plotted in a histogram to which a Gaussian function is fitted. Left (right): Phase difference measurements at SIS18 extraction (ESR injection). Middle: Measured phase difference of SIS18 and ESR at transfer. All histograms of identical scaling. Details see text.
The figure above shows the result of 8833 transfer between SIS18 and ESR. The leftmost and rightmost figure demonstrate the quality of phase measurements for each ring. Due to the nature of the sub-ns phase measurement, the achieved precision mainly depends on chosen revolution frequency. In general, a two-sigma value of less than 200 ps can be achieved. This is not a new finding, but has already demonstrated here. However, this is the first time such measurements are done in the productive environment of the real accelerator facility.
The new type of measurement is shown in the figure in the middle. Here, the phase difference of the two h=1 group DDS signals is measured at the moment of transfer.
With a the ParamModi set-value of 597.318 ns subtracted, a Gaussian shaped distribution around 0 value is obtained. The 2-sigma value is below 300 ps and corresponds to about 0.072 degree (SIS18, h=1). Thus, in 95% of all transfers, the match between bunch and bucket is better than 4 cm in the longitudinal direction.
Another even more important aspect is the stability of the system. The worst outliers are only about 530 ps of the desired values, for all of the 8833 transfers.
A comparison between the sub-ns phase measurement and the old measurement procedure of 1ns precision is difficult. The main reason is, that the stability of the frequency chains in the facility is already in the low picoseconds (White Rabbit) and femto-seconds (BuTiS) range and very good. Thus, the measurements done with the White Rabbit timing system at its native granularity of 1 ns are basically without visible jitter. Thus, the sub-ns phase measurement not only improves the granularity, at which phase differences can be set with ParamModi but also allow for much better diagnostics, as illustrated in the figure below.
Figure: Measured phase differences. The differences are plotted in a histogram to which a Gaussian function is fitted. Left (right): Phase difference measurements at SIS18 extraction (ESR injection). Middle: Measured phase difference of SIS18 and ESR at transfer. All histograms of identical scaling. Details see text.
The figure above shows the result of 8833 transfer between SIS18 and ESR. The leftmost and rightmost figure demonstrate the quality of phase measurements for each ring. Due to the nature of the sub-ns phase measurement, the achieved precision mainly depends on chosen revolution frequency. In general, a two-sigma value of less than 200 ps can be achieved. This is not a new finding, but has already demonstrated here. However, this is the first time such measurements are done in the productive environment of the real accelerator facility.
The new type of measurement is shown in the figure in the middle. Here, the phase difference of the two h=1 group DDS signals is measured at the moment of transfer.
With a the ParamModi set-value of 597.318 ns subtracted, a Gaussian shaped distribution around 0 value is obtained. The 2-sigma value is below 300 ps and corresponds to about 0.072 degree (SIS18, h=1). Thus, in 95% of all transfers, the match between bunch and bucket is better than 4 cm in the longitudinal direction.
Another even more important aspect is the stability of the system. The worst outliers are only about 530 ps of the desired values, for all of the 8833 transfers.
A comparison between the sub-ns phase measurement and the old measurement procedure of 1ns precision is difficult. The main reason is, that the stability of the frequency chains in the facility is already in the low picoseconds (White Rabbit) and femto-seconds (BuTiS) range and very good. Thus, the measurements done with the White Rabbit timing system at its native granularity of 1 ns are basically without visible jitter. Thus, the sub-ns phase measurement not only improves the granularity, at which phase differences can be set with ParamModi but also allow for much better diagnostics, as illustrated in the figure below.
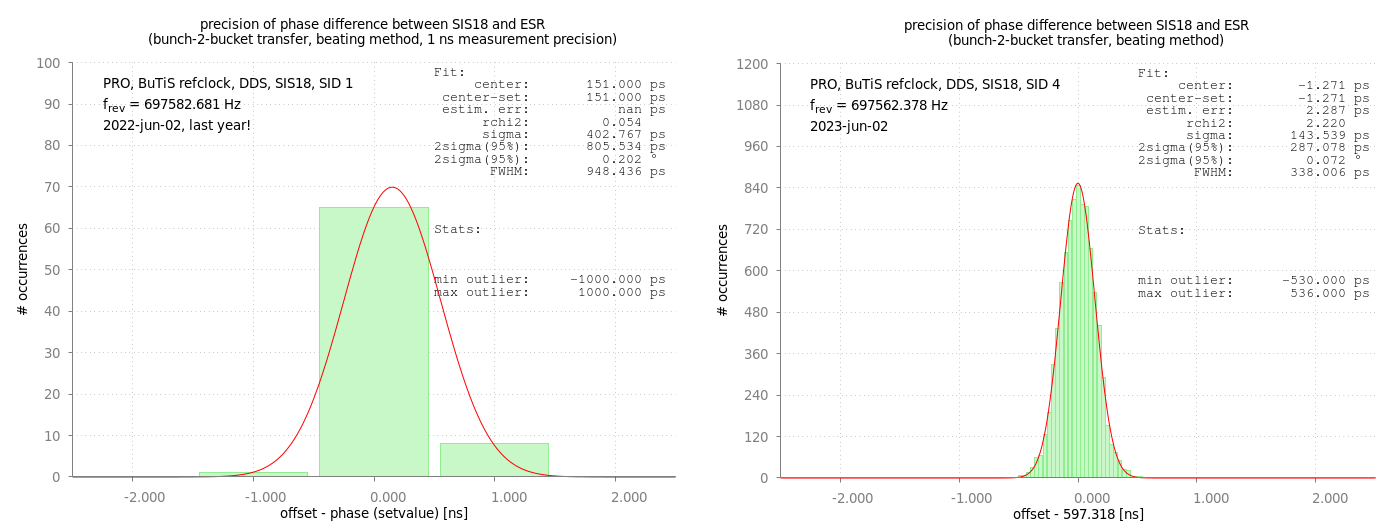 Figure: Measured phase difference for SIS18 and ESR at transfer. Left: machine experiment 2022 with 1 ns granularity. Right: dry-run 2023 with sub-ns precision. The y-axes of both histograms has a different scaling. Remartk: The figure on the right shows exactly the same as the middle figure in the previous graph; but it is differently scaled for a better comparison with the data from 2022 on the left.
The figure above only gives a qualitative impression. The numbers can not really be compared, as the statistics is different and also the beating time has been shorter in the machine experiment shown on the left side.
Figure: Measured phase difference for SIS18 and ESR at transfer. Left: machine experiment 2022 with 1 ns granularity. Right: dry-run 2023 with sub-ns precision. The y-axes of both histograms has a different scaling. Remartk: The figure on the right shows exactly the same as the middle figure in the previous graph; but it is differently scaled for a better comparison with the data from 2022 on the left.
The figure above only gives a qualitative impression. The numbers can not really be compared, as the statistics is different and also the beating time has been shorter in the machine experiment shown on the left side.
ESR -> CRYRING (YR)
The measurement was done from 2-5 June 2023. The following parameters were used- ESR
- Pattern ESR_EXP22_05_Au78_150-30-10_CRYRING_BB_MIT_Line
- Trev = 2450. 616587816 ns (true DDS value)
- CRYRING
- Pattern CRYRING_demo_2023_02_esr_prepost_fast
- Trev = 1225.585003998 ns (true DDS value)
- frequency beating
- h=2 (ESR) -> h=1 (CRYRING)
- period 5.428 ms
- phase difference per rf-period: 277 ps (0.081° @ h=2, ESR)
- multi-beat-tune = yes
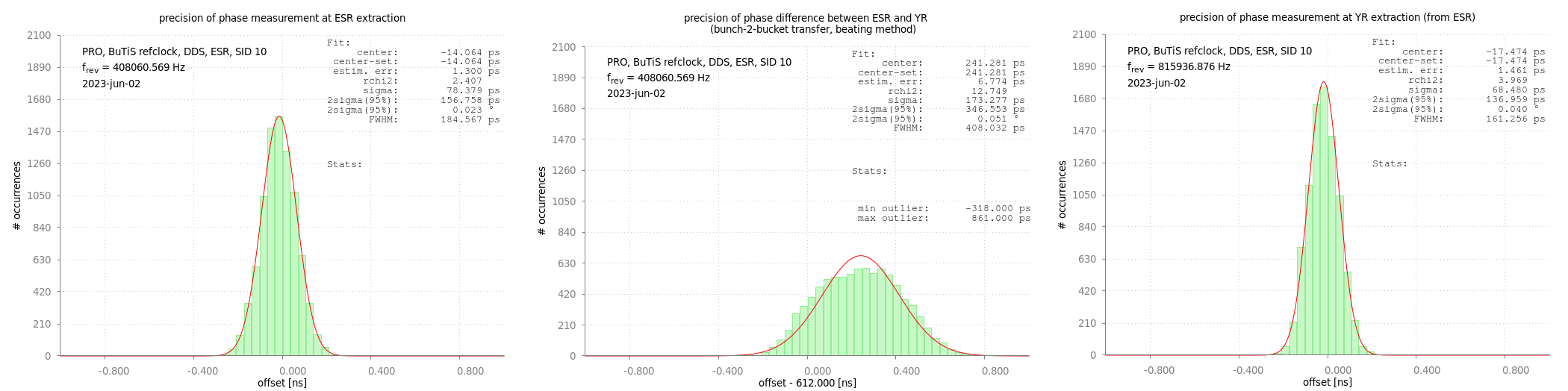 Figure: Measured phase differences. The differences are plotted in a histogram to which a Gaussian function is fitted. Left (right): Phase difference measurements at ESR extraction (CRYRING injection). Middle: Measured phase difference of ESR and CRYRING at transfer. All histograms of identical scaling. Details see text.
The figure above shows the result of 8835 transfer between ESR and CRYRING. The leftmost and rightmost figure demonstrate the quality of phase measurements for each ring. A two-sigma value of about 150 ps for both rings.
The precision of phase difference at transfer is shown in the figure in the middle. Here, the phase difference of the two h=1 group DDS signals is measured at the moment of transfer.
With a the ParamModi set-value of 614.??? ns subtracted, a Gaussian shaped distribution around 241 ps is obtained. Unfortunately, the data collection missed the sub-ns part of the ParamModi set-value due to a bug (the bug has been fixed in the meantime). This might explain, why the measured distribution is not centered at 0 but at 241 ps.
The 2-sigma value is below 350 ps and corresponds to about 0.051 degree (ESR, h=1). Thus, in 95% of all transfers, the match between bunch and bucket is better than 1.53 cm in the longitudinal direction.
The worst outliers are only about 600 ps from the center of the distribution, for all of the 8835 transfers.
Remark: For ESR to CRYRING, the absolute values seem to be slightly worse than for the transfer from SIS18 to ESR. However, the relative precision is in fact better as the frequencies are much lower for ESR to CRYRING.
Figure: Measured phase differences. The differences are plotted in a histogram to which a Gaussian function is fitted. Left (right): Phase difference measurements at ESR extraction (CRYRING injection). Middle: Measured phase difference of ESR and CRYRING at transfer. All histograms of identical scaling. Details see text.
The figure above shows the result of 8835 transfer between ESR and CRYRING. The leftmost and rightmost figure demonstrate the quality of phase measurements for each ring. A two-sigma value of about 150 ps for both rings.
The precision of phase difference at transfer is shown in the figure in the middle. Here, the phase difference of the two h=1 group DDS signals is measured at the moment of transfer.
With a the ParamModi set-value of 614.??? ns subtracted, a Gaussian shaped distribution around 241 ps is obtained. Unfortunately, the data collection missed the sub-ns part of the ParamModi set-value due to a bug (the bug has been fixed in the meantime). This might explain, why the measured distribution is not centered at 0 but at 241 ps.
The 2-sigma value is below 350 ps and corresponds to about 0.051 degree (ESR, h=1). Thus, in 95% of all transfers, the match between bunch and bucket is better than 1.53 cm in the longitudinal direction.
The worst outliers are only about 600 ps from the center of the distribution, for all of the 8835 transfers.
Remark: For ESR to CRYRING, the absolute values seem to be slightly worse than for the transfer from SIS18 to ESR. However, the relative precision is in fact better as the frequencies are much lower for ESR to CRYRING.
Conclusion
During winter 2022/2023 the sub-ns phase measurement method has been developed, implemented and deployed to the facility. The method offers the possibility to do measurements with a higher precision than provided by the native one-ns granularity of the White Rabbit timing system. This is beneficial for the the precision of the bunch-2-bucket system and allows for better diagnostics. Most importantly, the stability of the system has remained at a very good level. Even for a long measurement time of almost three days, the worst outliers are off-center by only about 3-sigma. N.B.: The findings are not only an achievement of the bunch-2-bucket system. B2B is an application on-top of the low-level RF-system and the White Rabbit Timing system. Hence, the result is mainly a demonstration of the precision and stability of BuTis and White Rabbit. Moreover, a single failure in data supply, frontend software, ramping and low-level RF-system would immediately show up either as an error during execution or as an outlier at the phase measurements. The results validate the stability of the overall control system. -- DietrichBeck - 20 Jun 2023| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
b2b-esr--yr-b2b-all.png | manage | 120 K | 2023-06-16 - 15:25 | UnknownUser | b2b_esr-cryging |
| |
b2b-sis18-esr-b2b-all.png | manage | 114 K | 2023-06-16 - 15:18 | UnknownUser | b2b_sis18-esr |
| |
b2b-sis18-esr_comparison_all.png | manage | 89 K | 2023-06-16 - 10:14 | UnknownUser | comparison old new |
Edit | Attach | Print version | History: r4 < r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r4 - 2023-06-20, dbeck
 Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding GSI Wiki? Send feedback | Legal notice | Privacy Policy (german)


